Dijous 31 de maig de 2018
Calcula l’àrea.
● D’un cercle de 5 cm de radi.
● D’un cercle de 4 m de diàmetre.
● D’una finestra circular de 30 cm de radi.
● D’una pizza de 14 cm de radi.
● D’una plaça de 200 m de diàmetre.
● D’un cràter circular de 300 m de diàmetre.
Dimecres 2 de maig de 2018
1. Copia el dibuix al teu quadern (cada metre serà un quadre del quadern) i després calcula l'àrea i el perímetre de la seguent figura.
2. Copia el dibuix al teu quadern i després calcula l'àrea i el perímetre de la següent figura.
3. Dibuixa l'escala d'unitats de distancia (metres) al teu quadern.
4. Dibuixa un rectangle al teu quadern on l'àrea sigui igual a 0,0016 Hm.
Dijous 26 d'abril de 2018
Dijous 19 d'abril de 2018
Dijous 22 de març de 2018
1. Expressa totes les mesures en la mateixa unitat i ordena-les de menor a major.
49,95 dm 0,05 hm 5,01 m 4.975 mm 502 cm 0,51 dam
2 En un formiguer hi ha 4 milions de formigues. Cada una fa 3 mm de llarg. Si es col·locaren totes en fila, sense deixar cap espai entre l’una i l’altra, la longitud de la fila seria major o menor de 10 km?
3. Un ferrer té 5 dam de cinta metàl·lica en un rotllo. L’ha tallat en trossos de 25 cm. Quants n’ha obtingut?
4. Un ciclista s’entrena en una pista coberta de 4 hm de llarg. Cada dia recorre 15 km i 600 m. Quantes voltes fa a la pista?
5. En fer una passa, Lluís recorre 82 cm. De casa a l’escola fa 800 passes. Quina distància en quilòmetres recorre?
Dijous 15 de març de 2018
Dimecres 14 de març de 2018
Calcula l’àrea.
● D’un cercle de 5 cm de radi.
● D’un cercle de 4 m de diàmetre.
● D’una finestra circular de 30 cm de radi.
● D’una pizza de 14 cm de radi.
● D’una plaça de 200 m de diàmetre.
● D’un cràter circular de 300 m de diàmetre.
Dimecres 2 de maig de 2018
1. Copia el dibuix al teu quadern (cada metre serà un quadre del quadern) i després calcula l'àrea i el perímetre de la seguent figura.
2. Copia el dibuix al teu quadern i després calcula l'àrea i el perímetre de la següent figura.
3. Dibuixa l'escala d'unitats de distancia (metres) al teu quadern.
4. Dibuixa un rectangle al teu quadern on l'àrea sigui igual a 0,0016 Hm.
Dijous 26 d'abril de 2018
1. Volem emmarcar un quadre de dimensions totals
103 cm de base per 63 cm d’altura. Quina longitud haurà de tenir la motllura
que volem utilitzar? Si la motllura costa 7,2 euros el metre, calcula el preu
del marc.
2. En una ciutat hi ha un parc en forma de
pentàgon irregular. Els costats mesuren respectivament, 45, 39, 29, 17 i 39
metres. Quina longitud té la tanca que l’envolta?
3. S’ha d’enrajolar el pati interior d’un edifici
amb rajoles quadrades de 30 cm de costat. El pati és rectangular i les seves
mesures són 10 m per 12 m. Quantes rajoles es necessitaran?
4. Una vela triangular d’una barca s’ha fet malbé
i s’ha de substituir per una altra. Per confegir la nova vela, ens cobren 21
euros per m2 . Quant valdrà la nova vela si ha de tenir 8 m d’altura i 4 m de
base?
5. Un rotllo de tela de 2 m d’amplada s’ha
utilitzat per tallar 1050 mocadors quadrats de 20 cm de costat. Quina longitud
de tela hi havia en el rotllo si no ha faltat ni sobrat tela?
6. Hem fabricat un estel, que té forma de rombe, i
les diagonals mesuren 393 cm i 205 cm respectivament. Per fer-lo, s’ha
utilitzat una làmina plàstica rectangular de longitud i amplada iguals que les
de l’estel. Calcula l’àrea de l’estel i de la làmina.
7. Resol:
a) Quants dam2 són 97 hm2 ?
b) Quants dm2 són 172 dam2 ?
c) Quants cm2 són 0.5 km2 ?
d) Quants dm2 són 2 km2 ?
e) Quants mm2 són 256 m2 ?
8. Resol
a) Quants m2 són 250000 mm2 ?
b) Quants dam2 són 6 m2 ?
c) Quants hm2 són 1423 mm2 ?
d) Quants km2 són 8000 dm2 ?
e) Quants m2 són 1500000 cm2 ?
Dijous 19 d'abril de 2018
1. Expressa totes les mesures en la mateixa unitat i ordena-les de menor a major.
49,95 dm 0,05 hm 5,01 m 4.975 mm 502 cm 0,51 dam
2 En un formiguer hi ha 4 milions de formigues. Cada una fa 3 mm de llarg. Si es col·locaren totes en fila, sense deixar cap espai entre l’una i l’altra, la longitud de la fila seria major o menor de 10 km?
3. Un ferrer té 5 dam de cinta metàl·lica en un rotllo. L’ha tallat en trossos de 25 cm. Quants n’ha obtingut?
4. Un ciclista s’entrena en una pista coberta de 4 hm de llarg. Cada dia recorre 15 km i 600 m. Quantes voltes fa a la pista?
5. En fer una passa, Lluís recorre 82 cm. De casa a l’escola fa 800 passes. Quina distància en quilòmetres recorre?
Dijous 15 de març de 2018
1.
Calcula aquestes longituds amb metres.
a.
2 hm i 5 dam + 4 km i 2 hm
b.
7 dam i 20 dm + 40 dm + 200 cm
2.
Joan necessita oli pels seus dos cotxes un verd i l’altre blau. Per el verd necessita
3 dl i 75 ml , i per el blau 13 cl i 5 ml. Quants ml necessita en total? Tindrà
suficient amb un llauna de mig litre?
3. El Pirata Barba Plata ha arribat a
la illa del Coral per buscar un tresor. En el mapa posa que, des de la riba, ha
de recórrer 3,7 hm a peu coix cap al
centre de la illa, i després altres 8,5 dam donant volteretes en la mateixa
adreça. Quants metres recorrerà en total des de la riba fins al tresor?
Expressa el resultat també en quilòmetres
4.
Quin pèl més bonic té Gabriela!
Abans era la noia que més llarg tenia el pèl de tota la classe: la cabellera li
mesurava 6 decímetres de longitud. Però ahir l'hi va tallar 25 centímetres,
així que ara la noia amb el pèl més llarg de la classe és María. Quants
centímetres mesura la cabellera de Gabriela ara? Expressa el resultat també en
mil·límetres
5. Un ós al que li encanta la mel vol treure mel d'un rusc que hi ha en la
branca d'un arbre, però està massa alta. Per aconseguir-la, es puja en una roca
de 12 dm d'alt que hi ha just sota i, amb les arpes molt estirades, arriba just
a agafar-la. Si aquest ós quan s'estira mesura exactament 2,3 m, a quina
distància del sòl estava exactament el rusc?
Dimecres 14 de març de 2018
- On els interessa comprar la gàbia, la roda i el abeurador per aconseguir el preu total més barat?
- Na Glòria ha llegit a Internet que el terra de la gàbia ha de cobrir-se amb serradures de fusta i canviar-les cada dia.
Quants quilograms de serradures han comprat en total?
- Si l'abeurador té una capacitat de 200 cm3, quants de litres d'aigua necessitaran per 15 dies?
Dimecres 28 de febrer de 2018
En el nostre dia a dia, ens trobem davant diferents unitats de longitud, massa i capacitat.
Per exemple, quan agafem l'autobús o el cotxe per anar fins a Vila, sabem que hem de recòrrer un total de 15km aproximadament. Però... sabríem dir quants metres (m) són? I si ho mesuressim amb un regle... quants centímetres (cm) mesuraria aquesta distància?
Això també ho podem aplicar a un brick de llet (que normalment són de 1 litre). Sabem dir quants mililitres (ml) serien? I amb una bossa de taronges que pesen 2kg. Quants grams (g) serien?
Anem a veure-ho!
Unitats de longitud.
La unitat bàsica de longitud és el metre (m), que es simbolitza amb la lletra m. Els múltiples i submúltiples són:
Nom símbol
Kilòmetre km
hectòmetre hm
decàmetre dam
metre m
decímetre dm
centímetre cm
mil·limetre mm
A continuació, veurem la regla que utilitzem per a convertir una unitat a una altra.
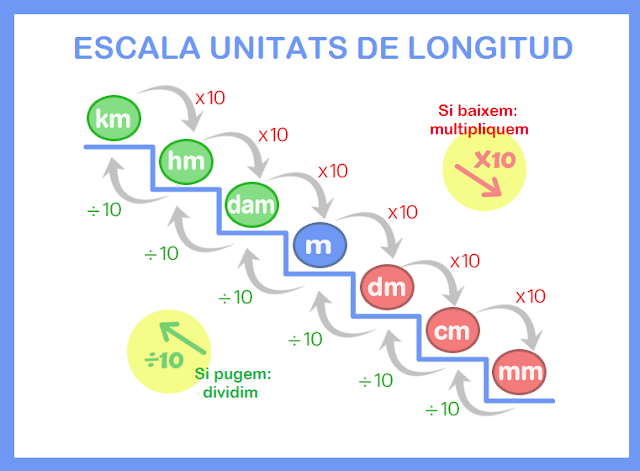
ACTIVITATS:
1. Passa les següents longituds a metres (m):
12 dam
23 km
4122 dm
65432 cm
234mm
2. Passa les següents longituds a quilòmetres (km):
145 dam
85 m
126 hm
0'83 dm
0'291 cm
763 mm
Unitats de massa
La unitat bàsica de massa és el gram (g), que es simbolitza amb la lletra g. Els múltiples i submúltiples són:
Nom símbol
Kilògram kg
hectògram hg
decàgram dag
gram g
decígram dg
centígram cg
mil·ligram mg
En el mateix cas, multiplicarem i dividirem per 10 seguint l'escala.
ACTIVITAT
Passa les diferents masses a la unitat que s’ indica:
31 dg = ________ g
21 cg = ________ dag
54 mg = _________ hg
67 dg = __________ dag
76 kg = __________ dag
Unitats de capacitat
La unitat bàsica de capacitat és el litre (l), que es simbolitza amb la lletra l. Els múltiples i submúltiples són:
Nom símbol
Kilòlitre kl
hectòlitre hl
decàlitre dal
litre l
decílitre dl
centílitre cl
mil·lilitre ml

ACTIVITAT
Passa les diferents capacitats a les unitats que indica:
42 dl = __________l
33 cl = __________ dal
212 cl =__________ hl
68 dal = __________dl
91 ml = ___________dal
Dijous 15 de febrer de 2018
Dimecres 7 de febrer de 2018
Dimecres 31 de gener de 2018
1. Completa la taula i després defineix els conceptes indicats:
8. Anota el
nombre que representa cada potència de 10:
Dijous 24 de gener de 2018
Video sobre els nombres mayas.
Dimecres 23 de gener de 2018
1. Observa la següent taula i contesta les preguntes.
Deures de nadal:
Dimecres 20 de desembre de 2017
Problemes regla de tres:
Dijous 7 de desembre de 2017
Dijous 29 de novembre de 2017
Dijous 23 de novembre de 2017
Dijous 16 de Novembre de 2017
Dimecres 15 de Novembre de 2017
La moda en estadística es el valor més repetit
La mitjana és el valor resultant de sumar tots els valors i aquest dividir-lo pel número de valors sumats.
Activitat: fixa't bé amb el següent gràfic i contesta a les preguntes:
1. Quin és el tenista amb més trofeus?
2. Quins tenistes han guanyat més Masters 1000?
3. Quants jugadors han guanyat una medalla olímpica?
4. Quants Grands Slams té John McEnroe?
5. Quin és l'únic jugador que no ha guanyat encara cap Word Tour Final?
Actividad 2: Copia al quadern i omple la segûent taula:
Dimecres 8 de Novembre de 2017
1. Calcula, amb calculadora, la mitjana de temperatures i de P. Atm.?
2. Quin és el valor que més es repeteix de les dades de temperatura i de P. Atm.?
Dimecres 25 d'octubre de 2017
Dimecres 18 d'octubre 2017
1. Resol aquestes operacions.
Dimecres 11 d'octubre de 2017
Feina classe:
Resol aquests problemes. Després, escriu en una sola expressió totes les operacions que hages fet.
Deures pel pont:
Dijous 05 d'octubre de 2017
1. Quin és el dia que es van registrar les màximes temperatures?
2. Quina és la màxima temperatura?
3. Quin és el dia que es van registrar les mínimes temperatures?
4. Quina és la temperatura mínima?
5. Quina és la diferència entre la màxima i la mínima temperatura?
6. Quina és la mitjana de temperatures?
dimecres 04 d'octubre de 2017.
42 dl = __________l
33 cl = __________ dal
212 cl =__________ hl
68 dal = __________dl
91 ml = ___________dal
Dijous 15 de febrer de 2018
Dimecres 7 de febrer de 2018
11. Expressa els
següents nombres utilitzant potències de base 10.
2.000
|
2 x 1.000
|
2 x 103
|
5.000.000
|
||
4.000.000.000
|
||
7.000.000
|
12. Escriu la
descomposició en suma de potències en base 10.
34.709
|
30.000 + 4.000 + 700 + 9
|
3 x 104+ 4 x 103 + 7 x
102+ 9
|
50.966
|
||
795.300
|
||
3.790.203
|
13. Escriu el número
que correspon a cada una de les següents descomposicions.
6 x 104 + 1 x 103 + 2 x 102 + 9 x 10 =
3 x 106 + 7 x 105 + 2 x 104 + 2 x 103=
8 x 105 + 9 x 104 + 3 x 103 + 5 x 10 + 1=
1 x 106 + 3 x 103 + 9 x 102 + 2 x 10 =
1 x 106 + 3 x 103 + 9 x 102 + 2 x 10 =
Dimecres 31 de gener de 2018
1. Completa la taula i després defineix els conceptes indicats:
Potència
|
Base
|
Exponent
|
Producte
|
Es llegeix
|
45
|
||||
7
|
3
|
|||
Sis elevat a
quatre
|
||||
3 x 3 x 3 x 3 x 3
|
2. Completa la taula.
12
|
22
|
32
|
42
|
52
|
62
|
72
|
82
|
92
|
102
|
3. Expressa com el
quadrat d'un nombre les següents situacions:
a.
Nombre de cromos si Emilio compra 5 sobres amb
5 cromos cadascun.
b.
Nombre de flors si Maite fa 17 rams amb 17
flors cadascun.
c. Nombre de trossos de
empanada si Arturo part 6 empanades en 6 trossos cadascuna.
4. Expressa aquestes potencies en forma de multiplicació i calcula'n el resultat.
63, 35, 92, 26, 19, 54
5. Calcula els següents quadrats:
63, 35, 92, 26, 19, 54
5. Calcula els següents quadrats:
302 = ................................................... 2002
= ..................................................
702 = ................................................... 6002
= ..................................................
6. Completa i calcula els cubs següents:
El cub de
10 és ....... = .....
x ..... x .....
= ................
El cub de
8 és ......... = .....
x ..... x .....
= ................
El cub de
20 és ....... = .....
x ..... x .....
= ................
El cub de
30 és ....... = .....
x ..... x .....
= ................
7. Escriu cada nombre en forma de
potència de 10:
1.000.000 = ................... 100.000 = ............. 100
= ................
1.000.000.000 = ............. 10.000 = ............... 1.000
= ............
105 = ..................................... 109 = .......................................... 106 = ....................................
9. Escriu cada nombre amb potències de 10:
160.000 = ................. 98.700 = ...................... 123.000.000
= ..................
10. Anota els nombres amb totes les seves xifres:
56 x 105 = ......................................................... 3.004 x 104 = ......................................................
711 x
109 = ........................................................ 909 x 107 = ----------------------------------------------------Dijous 24 de gener de 2018
Video sobre els nombres mayas.
Dimecres 23 de gener de 2018
- Escriu els següents nombres amb l'alfabet maya
- 27, 75, 125, 640, 1300, 2020.
- Esbrina el valor decimal dels següents nombres escrits en numeració maya.
- Omple la següent taula
Nombre decimal
|
Nombre romà
|
Nombre egipci
|
Nombre maya
|
|
Dies que
té un any
|
||||
Edat d’un
de vosaltres
|
||||
Nombre d’alumnes
de l’aula
|
||||
Any actual
|
.
|
Historia de los números
Si estás buscando la respuesta a la pregunta ¿Quien inventó los números?, después de leer este artículo verás que no existe una respuesta única ni tampoco clara. Pero de todos modos, vamos a explicarte cuál es el origen de los números.
¿Es más antigua la escritura que la numeración? No hay evidencia documental de escritura hasta el 2200 a.C. De esa fecha son las tablillas de barro cocido halladas en las ciudades babilónicas de Susa y Uruk, hoy la ciudad iraquí de Warka.
La numeración egipcia
No obstante esto, parece que los egipcios se adelantaron en casi un milenio, ya que en tiempos de la primera dinastía este pueblo contaba con un sistema decimal funcional que podía seguir el cómputo de hasta millones de unidades. Se le denomina sistema numeral hierático.
Existía una serie de símbolos o signos separados para cada número hasta el nueve y para cada potencia de 10. No obstante, no conocieron el número cero.
Así, el número 4 eran cuatro rayitas y el 10 una “U” invertida. Ello hizo que tuvieran que utilizar más signos que hoy para expresar las mismas cantidades: para escribir ’98’ ponían ocho rayas y nueve símbolos del número 10.
La numeración babilónica
La numeración primitiva no era decimal, no tenía como base la decena. El sistema babilónico, utilizado aproximadamente sobre el 1800 a.C. tenía como referente el número 60, y fue por ello por lo que el cómputo del tiempo se ciñó a esa unidad de medida. Inicialmente, no existía el número 0.
Pero fue también la numeración babilónica perfeccionada en el siglo IV a.C., la que creó el concepto y uso del número 0. Podía ponerse al principio, es decir, a la izquierda. También podía ser insertado en medio de una cantidad, en el interior de un número dado, pero curiosamente no podía figurar al final.
La numeración China
Otra de las culturas más antiguas también tenía su propio sistema de numeración que, igual que los egipcios, era con base en 10. Los diferentes símbolos se componían por agrupaciones de potencias de 10 y se escriben de arriba hacia abajo o de izquierda a derecha y no agrupados. Los símbolo que utilizaban tenían distintivos para su empleo doméstico o comercial. Se necesitaba tener cuidado en cómo agrupar los símbolo porque podían confundirse las unidades, como en el 57 y 75, ya que se escribían de la misma forma.
La numeración griega
Otra de las culturas más antiguas también tenía su propio sistema de numeración que, igual que los egipcios, era con base en 10. Los diferentes símbolos se componían por agrupaciones de potencias de 10 y se escriben de arriba hacia abajo o de izquierda a derecha y no agrupados. Los símbolo que utilizaban tenían distintivos para su empleo doméstico o comercial. Se necesitaba tener cuidado en cómo agrupar los símbolo porque podían confundirse las unidades, como en el 57 y 75, ya que se escribían de la misma forma.
La numeración griega
Hacia el 500 a.C., los griegos utilizaban ya, como números, las letras de su alfabeto. Se denominaba sistema acrofónico o ático.
De este modo, la letra a = 1. Este sistema carente de ceros se empleó durante mil años. Los judíos primero y los árabes más tarde lo adaptaron a sus propios alfabetos.
Ya por aquel tiempo, al no existir todavía las calculadoras, las cuentas se hacían con en el ábaco, un aparato manual consistente en varias hileras de pequeñas piedras móviles ensartadas, de donde derivó el término “cálculo”, del latín calculus = piedrecita.
La numeración romana
Los romanos mejoraron el sistema numérico introduciendo nuevos números, como por ejemplo el 5, el 50 y el 500: que corresponden a las letras V, L y D respectivamente.
Establecieron asimismo una novedad importante: la colocación de un símbolo delante o detrás de otro de mayor valor restaba o se sumaba a éste: XL era 50 – 10, y LX era 50 + 10.
Pero este sistema de dar a las letras valor numérico dificultaba la realización de operaciones aritméticas y multiplicar grandes cantidades resultaba imposible.
La numeración mayas
En la civilización amerindia de los mayas la base era el número 20: los dedos de pies y manos. Fue el primer pueblo en emplear el 0, que más que un número era un concepto no operativo.
Los números mayas se leían de abajo arriba, se escribían en columnas y utilizaron la base 20. No se conoce representación gráfica de su numeración anterior al siglo III de nuestra era.
.
Dijous 11 de gener de 2018
1. Observa la següent taula i contesta les preguntes.
19 Desembre de 2017
|
|||
billet/moneda
|
núm.
|
subtotal €
|
Tant per cent
|
5
|
6
|
||
2
|
29
|
||
1
|
92
|
||
0,5
|
39
|
||
0,2
|
23
|
||
0,1
|
19
|
||
0,05
|
17
|
||
0,02
|
7
|
||
0,01
|
10
|
||
Total
|
|||
- Calcula els subtotals de cada billet/moneda.
- Calcula el total del la setmana.
- Fes un gràfic de barres amb les dades de la taula anterior.
- Calcula el tant per cent que s'ha ingressat de cada moneda.
Deures de nadal:
1.
La directora de l'escola vol conèixer els
resultats de les eleccions de president del Centre de Pares i mares de l’escola.
Per a això va organitzar les dades en la següent taula. Observa-la i contesta les
preguntes.
Nom
|
Vots
|
Ramon
|
157
|
Juana
|
192
|
Monica
|
62
|
a)
Qui va guanyar les eleccions?
b)
Quantes persones varen votar en total?
c)
Quants vots més va tenir na Juana que en Ramon?
2.
El veterinari del zoològic necessitava fer un
registre amb les alçades d'alguns animals. Per a això va realitzar el següent
gràfic. Busca la informació que et permetrà contestar les preguntes.
a.
Quant més alta és la girafa que l’elefant?
b.
Quin animal és més alt que el lleó però més baix que l’elefant?
3.
Fes un gràfic lineal amb les següents dades.
Dies de la setmana
|
Temperatura
|
Dilluns
|
23
|
Dimarts
|
23
|
Dimecres
|
21
|
Dijous
|
23
|
Divendres
|
24
|
Dissabte
|
20
|
Diumenge
|
22
|
a.
Quin ha estat el dia més calorós?
b.
Quin dia ha fet més fred?
c.
Quina és la mitjana de les temperatures de la
setmana?
d.
Quina és la moda?
4.
A l'escola de David es va fer una enquesta per
saber quin tipus de pel·lícules prefereixen els estudiants. Usa la taula per
construir un gràfic de barres.
Tipus de pel·lícula
|
Acció
|
Terror
|
Bèl·liques
|
Comèdies
|
Ficció
|
Nº d’estudiants
|
72
|
69
|
47
|
57
|
76
|
80
|
|||||
70
|
|||||
60
|
|||||
50
|
|||||
40
|
|||||
30
|
|||||
20
|
|||||
10
|
|||||
0
|
Acció
|
Terror
|
Bèl·liques
|
Comèdies
|
Ficció
|
a.
Quin és el tipus de pel·lícula preferida pels
alumnes?
b.
Quina és el tipus de pel·lícula que menys els hi agrada?
Problemes
regles de tres:
5.
Un home ha comprat 2 síndries per 8 euros. Quant haurà
de pagar si en compra 50?
6.
Un cotxe fa 60 km en 30 minuts quants quilometres
farà en una hora?
7.
La classe de sisè guanya 6 euros venent 3
entrepans, Quant guanyarà si en ven 52?
Dimecres 20 de desembre de 2017
Problemes regla de tres:
1. Per 3 hores de feina, l’Albert ha cobrat 60
€, Quant cobrarà per 8 hores?
2. Dos obrers
descarreguen un camió en dues hores. Quant temps tardarien tres obrers?
3. Tres-cents grams de formatge valen 6€. Quants
grams podré comprar amb 4’50 € ?
4. Per 5 dies de feina he guanyat 390 €, Quant
guanyaria si treballés 18 dies?
5. Una màquina omple 240 ampolles en 20 minuts.
Quantes ampolles ompliria en una hora i mitja?
Dijous 7 de desembre de 2017
1.
Observa la població sobre els diferents municipis
d’Eivissa.
NOM
|
POBLACIÓ
|
Eivissa
|
49549
|
Sant Antoni
|
24478
|
Sant Josep
|
25889
|
Sant Joan
|
6070
|
Santa Eulària
|
36119
|
TOTAL
|
142105
|
a)
Calcula la població de cada municipi en tants per
cents.
b)
Fes el gràfic sectorial.
Dijous 29 de novembre de 2017
Dijous 23 de novembre de 2017
1.
De quin color són els teus ulls?
a.
El color dels meus ulls és
_____________________ .
2.
Cerca tots els companys de la classe que
tenguin el mateix color d’ulls que tu. Agrupa’t amb ells. (tots els que tenen
el color dels ulls marrons junts, els blaus junts, els verds junts, etc.).
3.
Contau-vos i després anotau-ho.
a.
El nombre d’alumnes de la classe que tenen el
color d’ulls ____________ és __________ .
4.
Després torna al teu lloc i anota tots els diferents colors d’ulls que hi ha dins l’aula. Ho hauras de preguntar. Recorda que si aixecam la mà per preguntar és més fàcil.
a.
El nombre d’alumnes de la classe que tenen el
color d’ulls ____________ és __________ .
b.
El nombre d’alumnes de la classe que tenen el
color d’ulls ____________ és __________ .
c.
El nombre d’alumnes de la classe que tenen el
color d’ulls ____________ és __________ .
d.
El nombre d’alumnes de la classe que tenen el
color d’ulls ____________ és __________ .
5.
Ara, omple el següent gràfic sectorial. Cada alumne/a
representa un sector.
6.
Quin és el color d’ulls és més comú (la moda)
_________________ .
Dijous 16 de Novembre de 2017
- Calcula la mitjana de l'altura i de la talla de les sabates dels companys del teu grup.
- Fes un gràfic de barres.
- Quina és la moda de la talla de les sabates de la classe?
Dimecres 15 de Novembre de 2017
La moda en estadística es el valor més repetit
La mitjana és el valor resultant de sumar tots els valors i aquest dividir-lo pel número de valors sumats.
Activitat: fixa't bé amb el següent gràfic i contesta a les preguntes:
2. Quins tenistes han guanyat més Masters 1000?
3. Quants jugadors han guanyat una medalla olímpica?
4. Quants Grands Slams té John McEnroe?
5. Quin és l'únic jugador que no ha guanyat encara cap Word Tour Final?
Actividad 2: Copia al quadern i omple la segûent taula:
NOM
|
ALTURA
|
TALLA SABATA
|
|
1
|
|||
2
|
|||
3
|
|||
4
|
- Calcula la mitjana de l'altura i de la talla de les sabates dels companys del teu grup.
- Quina és la moda de la talla de les sabates de la classe?
Dimecres 8 de Novembre de 2017
1. Calcula, amb calculadora, la mitjana de temperatures i de P. Atm.?
2. Quin és el valor que més es repeteix de les dades de temperatura i de P. Atm.?
Dimecres 25 d'octubre de 2017
1.
Escriu els següents nombres en lletres (català).
Recorda la norma D-U-C
a.
5.524
b.
27.369
c.
125.983
d.
108.046
2.
Realitza les operacions combinades.
a.
2
+ 3 * (4 + 5) – 12 =
b. (10
/ 5) + 9 / 3 - 3 =
c. 9
+ 12 / 4 - 3 * 3 =
d.
7
* 3 + 6 *4 – 5 =
e.
(5
+ 2) * (4 * 3) – (12/6) + 2 * 2 + 1 =
3.
Fes el gràfic representatiu de les notes d’una
classe representades en la següent taula.
Dia
|
nota
|
Alumne 1
|
7.25
|
Alumne 2
|
4.25
|
Alumna 3
|
8.5
|
Alumna 4
|
9
|
Alumna 5
|
6
|
Alumne 6
|
5
|
Alumna 7
|
5.5
|
Alumne 8
|
9.25
|
a) Quina és la nota mitjana de la classe?
b) Quina és la diferència entre la nota més alta i la més baixa?
b) Quina és la diferència entre la nota més alta i la més baixa?
4. Una classe ha obtingut, fent entrepans a l’escola,
15 monedes de dos euros, 20 monedes d’euro,
50 monedes de 50 cèntims i 5 monedes de 20 cèntims. Quant ha guanyat venent
entrepans? Expressa-ho amb una sola línia utilitzant operacions combinades.
5.
El primer dia del mes tenia al meu compte
1000 €. Aquell dia hi vaig ingressar 345 €. La setmana següent vaig treure’n
276 € i després vaig tornar a treure 193 €. L’últim dia del mes vaig ingressar
315 €. Quants diners em quedaven al final?
Dimecres 18 d'octubre 2017
1. Resol aquestes operacions.
- (13 - 9) x (26 + 13)
- 8 x (28 - 10) - (25 - 18)
- 70 - (26 - 9) x (58 - 32)
- 48 x (12 - 2) x 2 x 1
- 20 x (43 - 18) + 34 x 10
- 145 - (23 x 10 - 120) + 4 x 5
2. expressa els resultats dels entrepans del dimarts amb una sola fracció combinada.
| 2 | 1 | 0,5 | 0,2 | 0,1 | 0,05 | 0,02 | 0,01 |
| 43 | 90 | 45 | 52 | 50 | 8 | 0 | 0 |
Feina classe:
Resol aquests problemes. Després, escriu en una sola expressió totes les operacions que hages fet.
- Un camió portava 168 kg de fruita. En un mercat va descarregar 24 caixes de 3 kg de fruita cada una. Quants quilos de fruita porta ara el camió?
- Andreu va comprar uns pantalons per 18 € i una camiseta per 14 €. Va pagar amb un bitllet de 50 €. Quants diners li van tornar?
- Roser té una safata amb 35 pastissos de crema i 61 de xocolate. Els vol repartir en parts iguals en 8 plats. Quants pastissos ha de posar en cada plat?
Deures pel pont:
- Quantes camisetes i pantalons queden en total a la botiga quan tanca a la vesprada?
- Quants diners ha obtingut avui Joaquim per la venda dels vestits? Quants en podria haver obtingut si haguera venut tots els vestits que tenia
- El lot rebut consistia en caixes de 36 camisetes, caixes de 23 pantalons i caixes de 18 vestits. Quantes caixes contenia en total el lot?
- Un client compra 5 pantalons i algunes camisetes. Ha pagat 390 . Quantes camisetes ha comprat?
- Nicolau treballa en una obra col·locant taulells. Per a les parets d’una cuina tenia 21 caixes amb 24 taulells blancs cada una i 9 caixes amb 6 taulells de flors i 8 de fulles. Al final, li n’han sobrat 34. Quants taulells ha utilitzat?
Dijous 05 d'octubre de 2017
1. Quin és el dia que es van registrar les màximes temperatures?
2. Quina és la màxima temperatura?
3. Quin és el dia que es van registrar les mínimes temperatures?
4. Quina és la temperatura mínima?
5. Quina és la diferència entre la màxima i la mínima temperatura?
6. Quina és la mitjana de temperatures?
dimecres 04 d'octubre de 2017.
- Subratlla l’operació que has de fer en primer lloc. Després, calcula.
- 9 - 6 + 3 =
- 7 + 8 * 5 =
- 20 - 12 / 4 =
- 2 * 9 / 3 =
- 15 -(7 + 2) =
- (9 - 4) * 6 =
- 10 / (2 + 3) =
- (18 - 4) / 2 =
- Calcula.
- 8 + 12 / 4 =
- 10 / 5 * 3 =
- 2 * (6 + 9) =
- 24 - 2 * (7 + 3) =
- (10 - 4) + 18 / 6 =
- 12 / 3 + 5 * 8 =
- 6 - 5 + 4 * 2 - 7 =
- 9 + 8 / 4 - (1 + 3) =
- (4 + 2) * 5 + (8 - 6) =
- Una exposició d’art obri al públic 290 dies l’any. Cada dia la visiten 15 grups de 27 persones cada un. Quantes persones visiten cada any l’exposició?
- En una cursa es reparteix un total de 2.130 en premis. El guanyador del primer premi rep la meitat d’aquesta quantitat, el del segon guanya un terç del total i el del tercer s’emporta la resta. Quants diners rep el guanyador del tercer premi?
- En una granja han d’envasar 5.934 ous. Utilitzen 280 capses de 12 ous cada una i els restants els envasen en capses de 24 ous. Quantes capses de 24 ous omplin i quants ous els sobren?
dimecres 27 de setembre de 2017.
2. Observa el gràfic i resol.
En aquest pictograma s’ha representat el nombre de gelats que ha venut una parada de dilluns a divendres aquesta setmana.
- Quants gelats ha venut la parada aquesta setmana?
- La meitat dels gelats que van vendre dimarts i un terç dels gelats que van vendre dimecres eren de xocolate. Quants gelats de xocolate van vendre en total dimartsi dimecres?
- Cada gelat costa 2 euros. Quants diners van recaptar divendres més que dijous?
- Dissabte en van vendre el doble que dilluns i dimecres junts. Quants gelats van vendre dissabte?
dijous 21 de setembre de 2017.
Operacions bàsiques. realitzam diverses operacions divisions i multiplicacions.
dimecres 20 de setembre de 2017
corregim la prova inicial de la setmana passada.
dijous 14 de setembre de 2017
ALUMNE/A:
1. Escriu amb xifres els nombres següents:
Setanta-dos mil
cinc-cents catorze
|
|
Tres-cents vuit mil
dues-cents vint-i-quatre
|
|
Set milions quatre-cents
mil
|
2. Escriu
amb lletres:
485
|
|
3.105
|
|
3.274.096
|
3. Fes la descomposició dels següents nombres en
les seves unitats:
NOMBRES
|
DESCOMPOSICIÓ
|
1.503.872
|
1 milió + 5 centenes de miler + 0 desenes de
miler + 3 unitats de miler + 8 centenes + 7 desenes + 2 unitats
|
2.084.315
|
|
372.046
|
|
14.804
|
|
2.415
|
4. Ordena de més gran a més
petit les següents quantitats:
35 4.114 58.302 321 6.126.340
-----------------------------------------------------------------------------------------------------------
5. Col·loca i realitza les
següents operacions:
35 + 148 + 12575 =
45803 - 8397 =
4093 x 25 =
3765 : 5 =
48625 : 24 =
6. Representa les faccions:


1
|
3
|
4
|
4
|
7. Calcula les operacions amb
fraccions:
1
|
+
|
2
|
+
|
3 =
|
8
|
-
|
4
|
=
|
||||||||||||
6
|
6
|
|||||||||||||||||||
8
|
8
|
8
|
||||||||||||||||||
3
|
x
|
2
|
=
|
6
|
:
|
3
|
=
|
|||||||||||||
5
|
3
|
7
|
4
|
|||||||||||||||||
8. Completa:
|
1 any =
|
mesos
|
|
2 anys i mig =
|
mesos
|
|
5 setmanes i 4 dies =
|
deu
|
|
1 hora
|
=
|
minuts
|
½ hora
|
=
|
minuts
|
Tres quarts d’hora =
|
minuts
|
|
9. Posa els noms de les següents figures
geomètriques:

 |
|||||||||
 |
|||||||||
 |
|||||||||
 |
 |
||||||||
10.
Associa cada tipus de línia amb el seu nom:

Línia recta
Línia corba
Línies paral·leles
Línies perpendiculars
Segment


































Cap comentari:
Publica un comentari a l'entrada